구형파 푸리에 변환의 기본 개념과 활용 방법 (Basic Concepts and Applications of Spherical Fourier Transform)

구형파 푸리에 변환은 신호 처리 분야에서 자주 사용되는 변환 중 하나입니다. 이 변환은 시간 도메인에서 주기적인 신호를 주파수 도메인으로 변환하고, 이로 인해 해당 신호의 주기와 진폭을 파악하는데 매우 유용합니다. 이번 글에서는 구형파 푸리에 변환이 무엇인지, 어떤 원리로 작동하는지, 어떤 응용 분야에서 사용되는지 등에 대해 다루겠습니다. 또한 관련된 FAQ도 함께 제공하겠습니다.

1. 구형파 푸리에 변환이란 무엇인가?

구형파 푸리에 변환은 복소수를 사용하여 연속 신호를 주파수 도메인으로 변환하는 알고리즘입니다. 이 변환은 원래 푸리에 변환 방법의 확장이며, 범위가 제한되어있는 열개의 주기가 주어졌을 때 사용됩니다. 이로 인해 변환된 데이터는 복소수 형태로 나타납니다. 구형파 푸리에 변환도 DFT(Digital Fourier Transform)와 유사한 방식으로 작동하지만, 주파수 값이 매우 작거나 큰 경우 정확성이 떨어지는 단점이 있습니다.

2. 구형파 푸리에 변환의 원리는 무엇인가?

구형파 푸리에 변환은 원래 푸리에 변환 방법과 유사한 수식을 사용하여 주기적인 신호를 주파수 도메인으로 변환합니다. 다만, 변환할 신호가 제한된 범위의 주기를 가지는 신호일 경우, 이를 활용하여 공식을 조금 변경합니다. 공식은 다음과 같습니다.


여기서 N은 원래 푸리에 변환 방법과 같이 DFT를 수행하는 원소 수입니다. 구형파 푸리에 변환은 DFT처럼 복소수 평면을 사용합니다. 실제로 변환된 값은 주파수 매개 변수 k에 대한 두 개의 복소수 값입니다.

3. 구형파 푸리에 변환은 어떤 응용 분야에서 사용되는가?

구형파 푸리에 변환은 다양한 신호 분석 도구로 널리 사용됩니다. 이 변환은 신호 처리, 음향 학, 센서 데이터 분석 등과 같은 분야에서 활용됩니다. 구형파 푸리에 변환을 사용하면 주기적인 신호 주기와 주기의 변화를 파악하고 진폭, 주파수, 위상 등을 파악할 수 있습니다. 또한 이를 기반으로 주파수필터링 등 다양한 신호 처리 알고리즘을 적용하여 신호를 분석하고 필터링 할 수 있습니다.

4. 구형파 푸리에 변환을 사용하여 어떤 문제를 해결할 수 있는가?

구형파 푸리에 변환은 다음과 같은 문제를 해결할 수 있습니다.

– 신호의 주기성을 파악하여 예측 가능한 유용한 정보를 얻을 수 있습니다.
– 신호 중 주기를 가지고 있는 요소들을 분리하고, 데이터 분석 등에 활용할 수 있습니다.
– 신호 중 높은 주파수 성분(잡음 등)을 제거하여 정확도를 높일 수 있습니다.

FAQ

Q1. 구형파 푸리에 변환은 어떤 신호에 사용될 수 있는가?
A1. 구형파 푸리에 변환은 주기성을 가지는 신호에 사용됩니다. 이는 사인, 코사인 형태 등의 주기성 신호 뿐만 아니라, 음악 데이터 및 센서 데이터 등 다양한 응용 분야에서 사용될 수 있습니다.

Q2. 구형파 푸리에 변환과 DFT의 차이점은 무엇인가?
A2. 구형파 푸리에 변환과 DFT 모두 주파수 도메인 변환이지만, 구형파 푸리에 변환은 DFT처럼 푸리에 변환을 계산하지 않습니다. 구형파 푸리에 변환은 주기성을 가지는 신호에 대해 정확한 변환값을 얻을 수 있습니다. 반면 DFT는 모든 신호에 대해 정확한 변환값을 얻을 수 있지만, 높은 주파수나 낮은 주파수에서는 부정확함이 있을 수 있습니다.

Q3. 구형파 푸리에 변환은 어떻게 계산되는가?
A3. 구형파 푸리에 변환은 복소수를 사용하여 주기성을 가지는 신호를 주파수 도메인으로 변환하는 공식을 사용합니다. 변환된 데이터는 복소수 형태로 나타납니다.

Q4. 구형파 푸리에 변환의 주요 응용 분야는 무엇인가?
A4. 구형파 푸리에 변환은 주기성을 가지는 신호의 주기, 진폭 등을 분석하는 데 사용됩니다. 주요 응용 분야로는 음향학, 센서 데이터 분석, 신호 처리 등이 있습니다.

구형파 푸리에 변환 주제와 관련된 9개의 이미지를 찾았습니다.

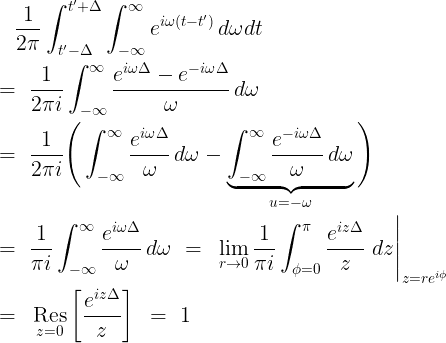
푸리에 변환(FFT: Fast Fourier Transformation)은 시간 도메인의 신호를 주파수 도메인으로 변환하는 알고리즘으로, 신호처리 분야에서 매우 중요한 역할을 합니다. 푸리에 변환은 오디오, 이미지, 비디오 등 여러 분야에서 사용되며, 특히 기계학습, 자연어 처리 등 분야에서 많이 활용됩니다. 이번 글에서는 푸리에 변환에 대한 예제를 중심으로 설명하겠습니다.

예제) 음성신호 분석

여러분은 음성신호를 처리하여 어떤 목적으로 사용할 수 있을까요? 예를 들어, 음성으로부터 발화자의 성별, 연령대, 기분 등을 분석하여 정보를 도출해낼 수 있습니다. 또한 음성에서 나타나는 음높이나 음조 등의 특징을 추출하여 음악 분석에 이용할 수도 있습니다. 이런 작업들을 위해서는 음성 데이터를 주파수 도메인으로 변환해야 합니다.

이를 위해 푸리에 변환 알고리즘을 사용하여 음성 신호를 주파수 영역으로 변환하고, 필요한 정보를 추출해내는 과정이 필요합니다. 다음은 파이썬으로 FFT를 이용해서 음성 신호 처리를 했던 예제입니다.

“`
import matplotlib.pyplot as plt
import numpy as np
import scipy.io.wavfile as wav

# 음성 파일 불러오기
rate, data = wav.read(‘test.wav’)

# FFT 수행하기
fft_out = np.fft.fft(data)
freqs = np.fft.fftfreq(len(data))

# FFT 결과 그래프 그리기
plt.figure()
plt.plot(freqs, np.abs(fft_out))
plt.xlabel(‘Frequency (Hz)’)
plt.ylabel(‘Amplitude’)
plt.show()
“`

위 코드에서 wav 모듈을 사용하여 음성 파일을 불러오고, np.fft.fft() 함수를 사용하여 FFT를 수행합니다. 이렇게 수행한 결과를 matplotlib 라이브러리를 사용하여 그래프로 나타냅니다.

FAQ

1. 푸리에 변환은 어떻게 동작하나요?

푸리에 변환은 주어진 시간 도메인 신호의 주파수 영역에서 생성된 복소수 값을 계산합니다. 이 과정에서 주어진 시간 도메인 신호를 주파수 도메인에서 분해하게 됩니다. 이 분해된 주파수 값은 복소수 값으로 계산되며, 진폭과 위상 정보가 포함됩니다.

2. 푸리에 변환을 왜 사용하나요?

푸리에 변환은 시간 도메인에서 복잡한 신호를 주파수로 분해할 수 있어서 많은 응용 분야에서 사용됩니다. 그 중에서도 오디오, 영상 처리, 기계 학습, 자연어 처리에서 사용됩니다.

3. 푸리에 변환을 할 때 입력값은 어떻게 결정되나요?

입력값은 주어진 시간 도메인의 신호값이며, 이는 연속 시간 신호냐 샘플 신호냐에 따라 다르게 결정됩니다. 연속 시간 신호의 경우 대표적으로 디지털 오실로스코프에서 신호를 측정할 때 사용되며, 샘플 신호의 경우 디지털 변환기에서 샘플링된 신호값을 사용합니다.

4. 파라메터 설정이 매우 중요하다고 하는데, 이는 어떤것들인가요?

FFT 수행 시 파라미터는 N, Fs, frequency range 등이 있습니다. N은 FFT를 수행할 때 사용할 샘플 수를 결정하며, Fs는 샘플링 주파수를 결정합니다. Frequency range는 FFT 결과에서 보고자 하는 주파수 범위를 설정합니다. 이 파라미터를 적절히 설정해야 원하는 분석 결과를 얻을 수 있습니다.

5. 푸리에 변환과 푸리에 역변환은 어떤 차이가 있나요?

푸리에 변환은 시간 도메인의 신호를 주파수 도메인으로 변환하는 것이고, 역변환은 주파수 도메인의 신호를 시간 도메인으로 변환합니다. 따라서, 푸리에 변환을 통해 얻은 주파수 영역의 정보를 활용하여 이를 다시 시간 도메인으로 복원하는데 사용할 수 있습니다.

푸리에 변환 표(Fourier Transform)란 이산 시계열 신호의 시간 도메인(time domain)을 주파수 도메인(frequency domain)으로 변환하는 수학적 기법으로, 이를 통해 시계열 데이터의 주파수 성분을 분석하고 이해할 수 있게 됩니다. 이 변환은 주로 음성, 영상, 통신 등 다양한 분야에서 사용되며, 제공되는 정보를 분석하고 처리할 수 있도록 돕습니다.

푸리에 변환은 1807년 프랑스의 수학자 조셉 프리에(Joseph Fourier)에 의해 처음 소개되었습니다. 그는 열 전달(heat transfer) 문제에 관한 연구에서 이 변환을 처음 적용했습니다. 이후, 이 변환은 공학, 물리학, 의료학 등 다양한 분야에서 사용되게 되었습니다.

이 변환을 사용하면 시간 범위(time domain)에서의 신호를, 주파수 범위(frequency domain)로 변환할 수 있습니다. 이 변환을 수행하면 얻어지는 결과값은 신호의 다양한 주파수 성분과 그에 따른 진폭(amplitude)과 위상(phase) 정보를 제공합니다. 이를 통해, 거시적인 데이터에서는 예상되지 않았던 주파수 성분이 발견될 수 있으며, 이 정보를 활용하여 상세한 분석이 가능해집니다.

이 변환을 수행하는 방법에는 DFT(Discrete Fourier Transform), FFT(Fast Fourier Transform) 등 다양한 방법이 있습니다. DFT는 N개의 숫자를 입력값으로 받아 N개의 주파수 성분을 출력하는 방법입니다. FFT는 DFT를 보다 빠르게 계산할 수 있는 알고리즘으로, N개의 입력값에 대해 O(NlogN) 시간 내에 주파수 성분을 계산할 수 있습니다.

푸리에 변환 표를 활용하면 다양한 시계열 데이터를 분석할 수 있습니다. 예를 들어, 음성 신호를 푸리에 변환 표에 적용하면 소리의 주파수 성분을 알 수 있고, 이를 활용하여 소리의 원인을 파악할 수 있습니다. 또한, 진동 신호를 분석하여 구조물의 안정성을 판단하는 등의 응용 분야에도 사용됩니다.

푸리에 변환 표는 여러 산업 분야에서 중요한 역할을 수행하고 있습니다. 특히, 신호 처리(signal processing) 분야에서는 빠르고 정확한 분석을 위해 필수적인 수단으로 활용됩니다. 이러한 이유로, 푸리에 변환 표는 다양한 연구와 산업 분야에서 꾸준히 사용되고 있습니다.

FAQ

Q: 푸리에 변환은 어떤 분야에서 사용되나요?
A: 푸리에 변환은 음성, 영상, 통신, 진동 등 다양한 분야에서 사용됩니다. 주로 시계열 데이터의 주파수 성분을 분석하고 처리하는데 활용됩니다.

Q: 푸리에 변환을 수행하는 방법은 무엇인가요?
A: 푸리에 변환을 수행하는 방법에는 DFT(Discrete Fourier Transform), FFT(Fast Fourier Transform) 등 다양한 방법이 있습니다.

Q: 푸리에 변환을 사용하여 어떤 정보를 얻을 수 있나요?
A: 푸리에 변환을 수행하면 시계열 데이터의 주파수 성분을 파악할 수 있습니다. 이를 통해, 거시적인 데이터에서는 예상되지 않았던 주파수 성분이 발견될 수 있으며, 이 정보를 활용하여 상세한 분석이 가능해집니다.

Q: 푸리에 변환 표는 어떤 역할을 수행하나요?
A: 푸리에 변환 표는 신호 처리 분야에서 빠르고 정확한 분석을 위해 필수적인 수단으로 활용됩니다.